Virksomhedens Omkostningsforhold

Effektiv styring af omkostninger er afgørende for enhver virksomheds succes. Dette kapitel vil give en dybdegående forståelse af forskellige omkostningstyper, deres opførsel og betydning for beslutningstagning. Vi vil se på, hvordan virksomheder kan analysere og styre deres omkostninger for at maksimere rentabiliteten.

I dette kapitel ser vi nærmere på:

Faste og Variable Omkostninger: Hvordan adskiller de sig, og hvilken betydning har det for virksomhedens økonomi?
Omkostningsforløb: Analyse af omkostningernes opførsel ved forskellige produktionsniveauer.
Enhedsomkostninger: Hvad koster det i gennemsnit at producere en enhed?
Grænseomkostninger: Hvad koster det at producere én enhed mere?
Beslutningsrelevante Omkostninger: Hvilke omkostninger skal indgå i beslutningsgrundlaget?
Produktionsmetoder: Hvordan vælges den mest effektive produktionsmetode?

Faste og Variable Omkostninger

Opdelingen af omkostninger i faste og variable er grundlæggende for omkostningsstyring. De to omkostningstyper reagerer forskelligt på ændringer i produktionsniveauet.

Virksomhed	Faste omkostninger (eksempler)	Variable omkostninger (eksempler)
LEGO	Fabrikker i Billund: 200 mio. kr./år	Plastik til klodser: 5 kr./kg
Tesla	Gigafactory i Berlin: 500 mio. kr./år	Batterier til elbiler: 15.000 kr./stk
Novo Nordisk	Produktionsanlæg i Bagsværd: 1.000 mio. kr./år	Insulin råvarer: 50 kr./dosis
Carlsberg	Bryggeriet i København: 150 mio. kr./år	Malt og humle: 3 kr./liter øl
H&M	Butiksleje Strøget: 1 mio. kr./år	Produktionsomkostning pr. t-shirt: 20 kr.
McDonald's	Restaurant franchise: 500.000 kr./år	Råvarer pr. Big Mac: 15 kr.

Faste omkostninger (FO):

Er omkostninger, der ikke ændrer sig når produktionsniveauet ændres
Eksempler: Husleje, fast løn til medarbejdere, forsikringer
Disse omkostninger forbliver konstante uanset om virksomheden producerer 100 eller 1000 enheder
Faste omkostninger er også kendt som kapacitetsomkostninger

Variable omkostninger (VO):

Er omkostninger, der ændrer sig når produktionsniveauet ændres
Eksempler: Råvarer, direkte arbejdskraft, energi
Stiger jo flere enheder der produceres
Variable omkostninger er også kendt som produktionsomkostninger, for produktionsvirksomheder
Variable omkostninger er også kendt som direkte omkostninger

Eksempel: Isbod

Lad os se på et konkret eksempel med en isbod for at forstå forskellen mellem faste og variable omkostninger:

Faste omkostninger (FO):

Er omkostninger, der ikke ændrer sig med mængden af solgte is
Forbliver konstante uanset om isboden sælger 100 eller 1000 is
Eksempler: Husleje, fast løn til medarbejdere, forsikringer

Variable omkostninger (VO):

Er omkostninger, der ændrer sig direkte med mængden af solgte is
Stiger jo flere is der sælges
Eksempler: Is, kugler, toppings, papirbægere

I nedenstående tabel ser vi et detaljeret overblik over de forskellige omkostningstyper og deres betydning for isboden:

Omkostningstype	Forkortelse (DK)	Forkortelse (EN)	Forklaring
Variable omkostninger	VO	VC (Variable Cost)	De omkostninger, der ændres i takt med den producerede eller solgte mængde. Disse omkostninger er direkte relaterede til produktionsniveauet. Måles i kr. pr. tidsperiode. Eksempler: Råmaterialer, direkte arbejdskraft, energi. Eksempel fra isbod: Is pr. kugle: 2 kr. Kugle: 1 kr. Toppings: 3 kr. Papirbæger: 1 kr. Her har VO et lineært forløb VO vokser med 7 kr. pr. is. dvs. hældningskoefficienten a er 7. Når vi sælger 0 is, er VO = 0 kr. dvs. b = 0. Funktionsforskriften for VO er således VO = aX + b = 7X + 0 = 7X
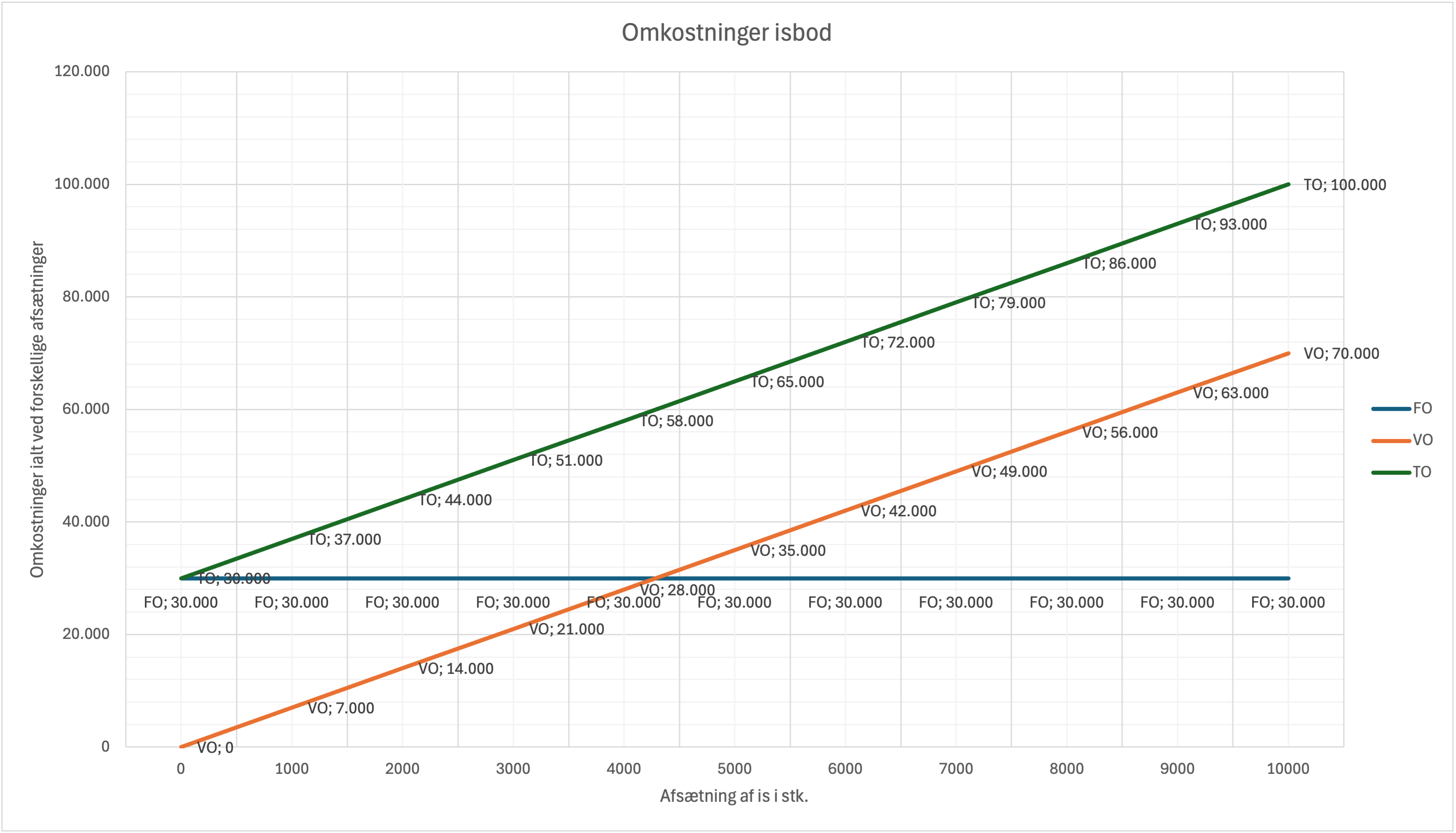
Faste omkostninger	FO	FC (Fixed Cost)	De omkostninger, der ikke ændres i takt med den producerede eller solgte mængde. Disse omkostninger forbliver konstante inden for en given kapacitetsgrænse. Måles i kr. pr. tidsperiode. Eksempler: Husleje, afskrivninger, fast løn. Eksempel fra isbod: Husleje: 5.000 kr. pr. måned Fast løn: 25.000 kr. pr. måned Total FO: 30.000 kr. pr. måned Her har FO et konstant forløb FO er konstant 30.000 kr. pr. måned. Funktionsforskriften for FO er således FO = aX + b = 0X + 30.000 = 30.000
Totale omkostninger	TO	TC (Total Cost)	De samlede omkostninger ved en given aktivitet i en given periode. Inkluderer både faste og variable omkostninger. Måles i kr. pr. tidsperiode. Formel: TO = FO + VO Eksempel fra isbod: Hvis der sælges 1000 is om måneden: FO: 30.000 kr. (husleje, fast løn) VO: 1000 × 7 kr. = 7.000 kr. (is, kugler, toppings) Total TO: 37.000 kr. Her har TO et lineært forløb TO vokser med 7 kr. pr. is. dvs. hældningskoefficienten a er 7. Når vi sælger 0 is, er TO = 30.000 kr. dvs. b = 30.000. Funktionsforskriften for TO er således TO = aX + b = 7X + 30.000 Vi ved også at TO = FO + VO = 30.000 + 7X Så begge metoder giver samme resultat.
Totale enhedsomkostninger	TE	ATC (Average Total Cost)	Totale omkostninger pr. enhed ved en given mængde. Repræsenterer den gennemsnitlige omkostning ved at producere én enhed. Måles i kr. pr. stk. Formel: TE = TO / Produktionsmængde Kaldes også totale gennemsnitsomkostninger. Eksempel fra isbod: Hvis der sælges 1000 is: TE = 37.000 kr. / 1000 = 37 kr. pr. is Vi får den generelle funktionsforskrift for TE = TO / X = (30.000 + 7X) / X = 30.000 / X + 7
Variable enhedsomkostninger	VE	AVC (Average Variable Cost)	Variable omkostninger pr. enhed ved en given mængde. Repræsenterer den gennemsnitlige variable omkostning ved at producere én enhed. Måles i kr. pr. stk. Formel: VE = VO / Produktionsmængde Kaldes også variable gennemsnitsomkostninger. Eksempel fra isbod: VE = 7 kr. pr. is (konstant) Vi får den generelle funktionsforskrift for VE = VO / X = 7X / X = 7
Faste enhedsomkostninger	FE	AFC (Average Fixed Cost)	Faste omkostninger pr. enhed ved en given mængde. Repræsenterer den gennemsnitlige faste omkostning ved at producere én enhed. Måles i kr. pr. stk. Formel: FE = FO / Produktionsmængde Kaldes også faste gennemsnitsomkostninger. Eksempel fra isbod: Hvis der sælges 1000 is: FE = 30.000 kr. / 1000 = 30 kr. pr. is Vi får den generelle funktionsforskrift for FE = FO / X = 30.000 / X
Grænseomkostninger	Gromk	MC (Marginal Cost)	Ændring i totale eller variable omkostninger ved en ændring i produktionens størrelse på en enhed. Repræsenterer den præcise omkostning ved at producere den sidste enhed. Måles i kr. pr. stk. Formel: Gromk = Ændring i TO / Ændring i mængde = ΔTO / ΔX Eller du kan beregne Gromk ud fra variable omkostninger VO: Gromk = Ændring i VO / Ændring i mængde = ΔVO / ΔX Eksempel fra isbod: Gromk = 7 kr. (Her er Gromk det samme som VE, da faste omkostninger ikke ændrer sig) Har man givet en funktionsforskrift for en omkostningsfunktion VO eller TO, kan man beregne Gromk ved at differentiere funktionsforskriften dvs. Gromk = VO'= TO' I vores isbod er funktionsforskriften for VO= 7X og TO = 30.000 + 7X - Vi kan så finde Gromk ved at differentiere funktionsforskriften for VO og TO Gromk = VO'= 17X^1-1 = 7X⁰ = 7 Gromk = TO'= 030.000X^0-1 + 17X^1-1 = 0 + 7 = 7 Vi får altså samme resultat Gromk = 7 kr. pr. is Husk matematik regnereglerne:* Potensregnereglerne X⁰ = 1 At differentiere betyder at man skal gange med eksponenten og trække 1 fra eksponenten, en konstant differentieres til 0 f(x) = axⁿ => f'(x) = nax^n-1 dvs. f.eks. f(x) = 2X³ => f'(x) = 32X^3-1 = 6X² f(x) = 5X⁴ => f'(x) = 45X^4-1 = 20X³ f(x) = 10 = 10X⁰ => f'(x) = 010X^0-1 = 0 Bemærk her er Gromk = VE, da VE er konstant 7 kr. pr. is. Men hvis VE er en lineær funktion, så kan Gromk hurtigt findes som VE med den dobbelte hældning, dvs. hvis: VE = aX + b, så er Gromk = 2aX + b.

Vigtige overvejelser for isboden:

For at være rentabel skal prisen pr. is være højere end de totale enhedsomkostninger (TE)
De faste enhedsomkostninger (FE) falder jo flere is der sælges, hvilket gør det billigere at producere hver is
Grænseomkostningerne (Gromk) er konstante på 7 kr. pr. is, da de variable omkostninger er lineære
For at nå break-even point skal isboden sælge nok is til at dække både de faste omkostninger (30.000 kr.) og de variable omkostninger (7 kr. pr. is)
En afsætning på 1000 is om måneden synes lav det er 33 is om dagen, det betyder at isboden skal sætte en meget høj salgspris pr. is for at være rentabel.
Virksomheden har relativt store faste omkostninger (30.000 kr. pr. måned), her ville en timelønsansat være en fordel, så kan man holde lukket når det regner eller er dårligt vejr.
Når vejret er godt, isboden måske øge personalet for at kunne håndtere den stigende efterspørgsel.

Eksempel: Isboden ved forskellige produktionsniveauer, med en fastansat.

Mængde X stk.	FO	FE	VO	VE	TO	TE	Gromk
0	30.000	-	0	-	30.000	-	7
1000	30.000	30	7.000	7	37.000	37	7
2000	30.000	15	14.000	7	44.000	22	7
3000	30.000	10	21.000	7	51.000	17	7
4000	30.000	7,5	28.000	7	58.000	14,5	7
5000	30.000	6	35.000	7	65.000	13	7
6000	30.000	5	42.000	7	72.000	12	7
7000	30.000	4,29	49.000	7	79.000	11,29	7
8000	30.000	3,75	56.000	7	86.000	10,75	7
9000	30.000	3,33	63.000	7	93.000	10,33	7
10000	30.000	3	70.000	7	100.000	10	7

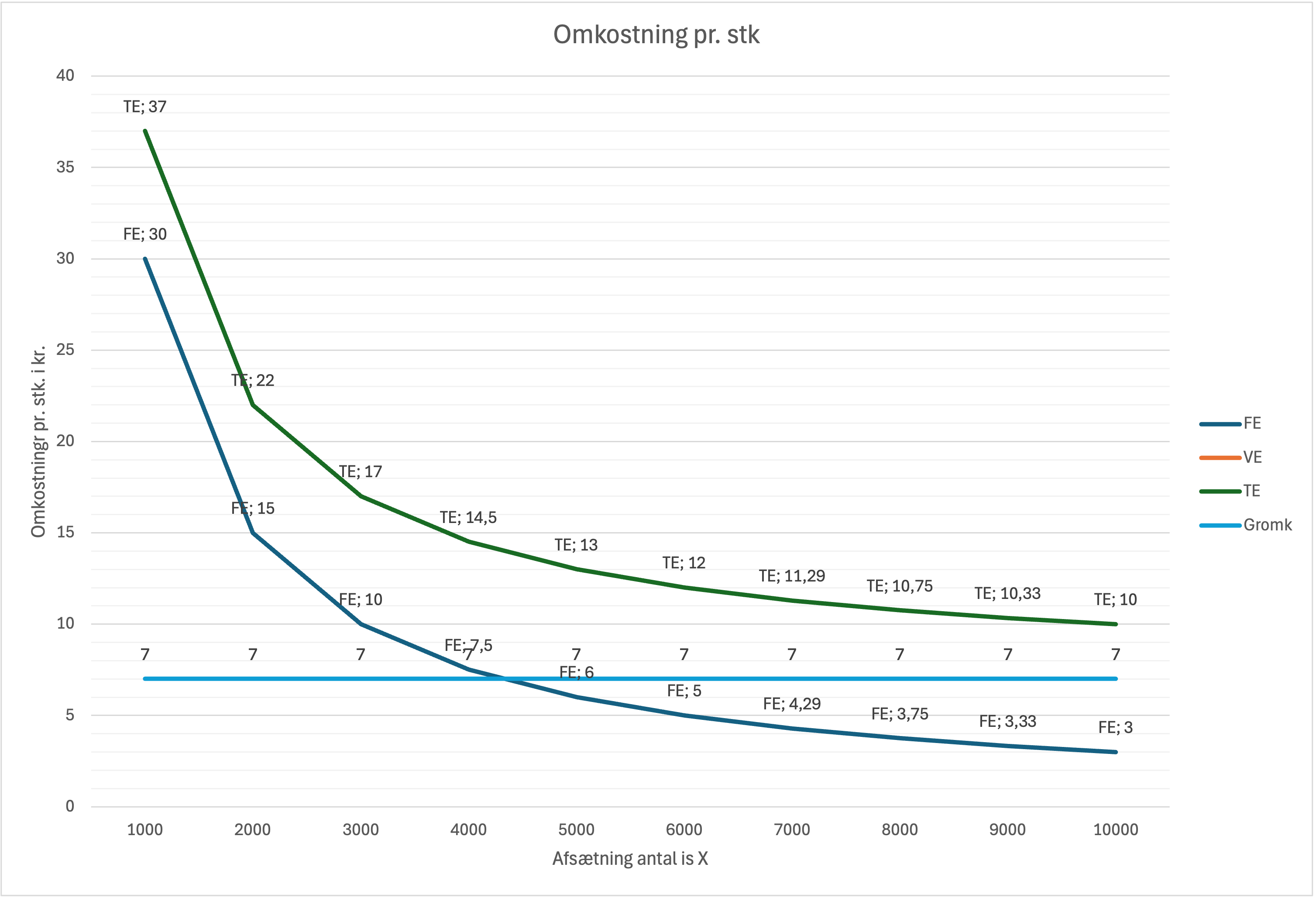
I dette eksempel med isboden er grænseomkostningerne konstante på 7 kr. pr. is, da de variable omkostninger er lineære, derfor ser vi kun en graf for Gromk (grænseomkostninger) på figuren da VE ligger bag denne graf.
Dette betyder, at det koster det samme at producere den første is som den sidste is. Dette er typisk for virksomheder med simple produktionsprocesser og konstante variable omkostninger pr. enhed.

Omkostningsforløb ved forskellige produktionsniveauer

Ved analyse af omkostningsforløbet kan vi se følgende mønstre:

Faste omkostninger (FO) forbliver konstante på 30.000 kr. uanset produktionsniveau
Variable omkostninger (VO) stiger lineært med 7 kr. pr. is
Totale omkostninger (TO) stiger lineært med 7 kr. pr. is, startende fra 30.000 kr.
Variable enhedsomkostninger (VE) forbliver konstante på 7 kr. pr. is
Faste enhedsomkostninger (FE) falder jo flere is der sælges
Totale enhedsomkostninger (TE) falder også med stigende produktion

Forskellige omkostningsforløb

I virkeligheden følger omkostninger sjældent en perfekt lineær kurve. Her er nogle praktiske eksempler på forskellige omkostningsforløb:

Virksomhed	Omkostningstype	Forløb	Forklaring
Netto	Mængderabat	Trappeformet faldende	0-1000 stk: 10 kr/stk 1001-5000 stk: 8 kr/stk 5001+ stk: 6 kr/stk
Carlsberg	Overarbejde	Trappeformet stigende	0-37 timer: 150 kr/time 38-45 timer: 200 kr/time 45+ timer: 250 kr/time
LEGO	Produktionsomkostninger	Lineært stigende	Stiger gradvist med 2 kr/stk for hver 1000 stk over 100.000 stk
H&M	Transportomkostninger	Lineært faldende	Falder med 0,5 kr/stk for hver 1000 stk over 5000 stk

Eksempel: Isbod med trappeformet stigende grænseomkostninger

Lad os se på en isbod, hvor grænseomkostningerne stiger ved overarbejde:

Mængde X stk. afsætningsinterval	Gromk
0-1000 stk.	7 kr
1001-2000 stk.	8 kr
2001+ stk.	9 kr

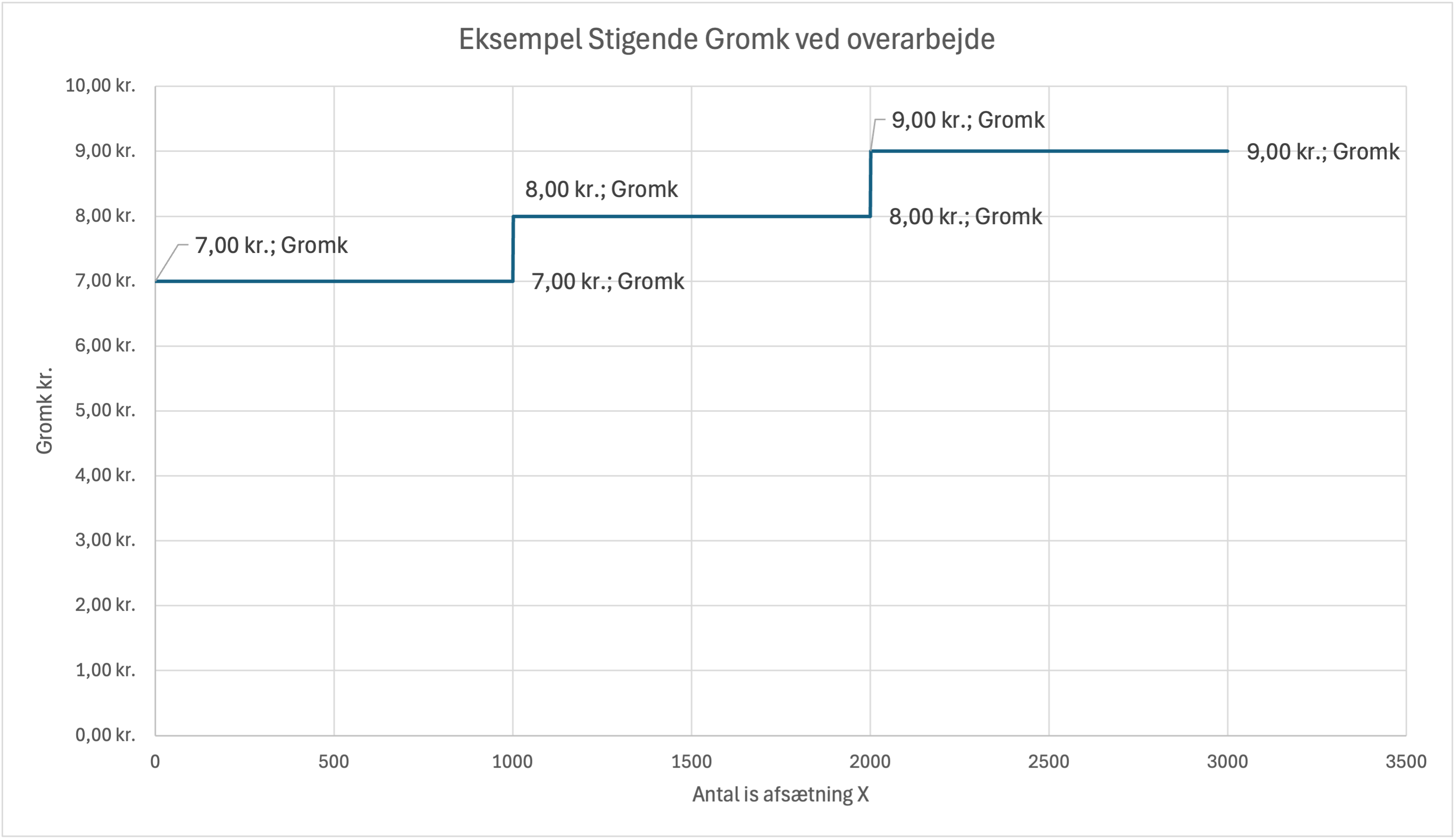
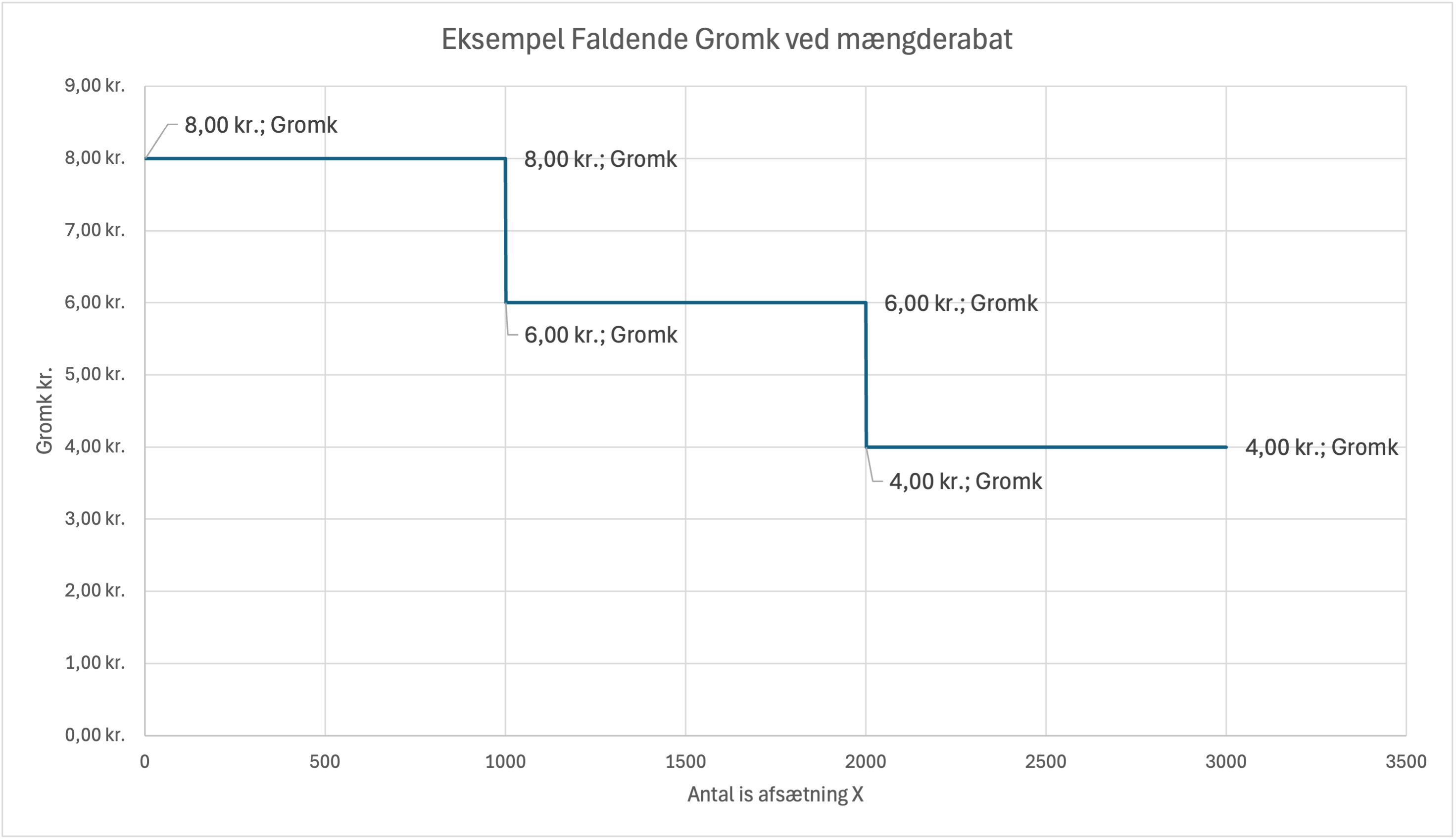
Eksempel: Isbod med trappeformet faldende grænseomkostninger

Nu ser vi på en isbod, hvor grænseomkostningerne falder ved mængderabat på is:

Mængde X stk. afsætningsinterval	Gromk
0-1000 stk.	8 kr
1001-2000 stk.	6 kr
2001+ stk.	4 kr

Eksempel: Isbod med lineært stigende grænseomkostninger

Her ser vi på en isbod, hvor grænseomkostningerne stiger gradvist liniært med produktionen:

Mængde X stk. afsætning	Gromk
0 stk.	5,5 kr
1000 stk.	7 kr
2000 stk.	8,5 kr
3000 stk.	10 kr

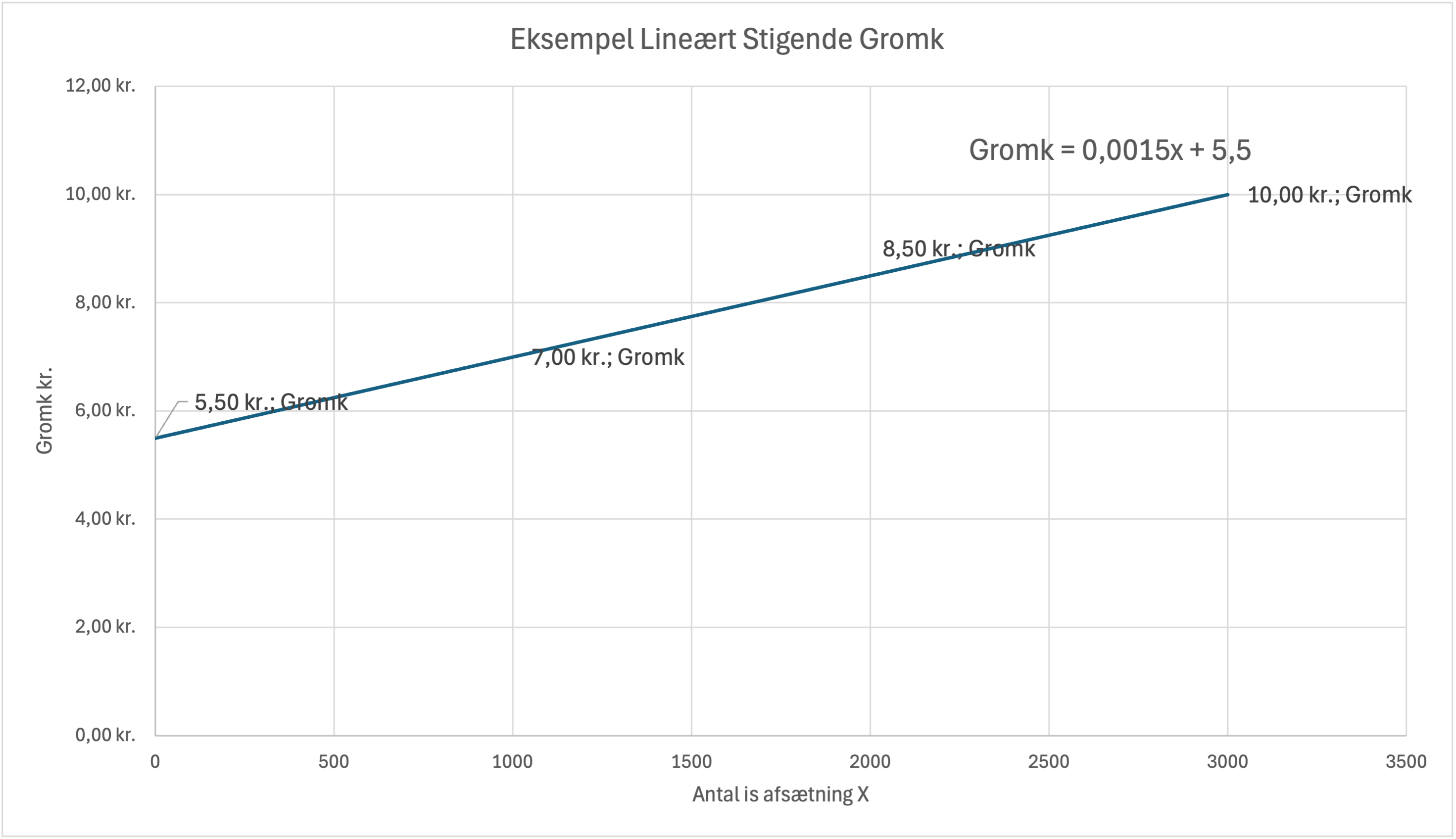
Vi kan bestemme funktionsforskriften for grænseomkostningerne ved at indsætte punkterne i f.eks. Excel og tilføje en trendlinje.
Vi kan også udregne funktionsforskriften når vi har to punkter.
Eksempelvis har vi punkterne (0,5,5) og (3000,10)
Vi indsætter punkterne i formlen for en lineær funktion y = ax + b
Vi får derved ligningen 5,5 = a*0 + b, hvor vi kan se, at b = 5,5
Vi får derved ligningen 10 = a*3000 + 5,5, hvor vi kan løse for a
a = (10-5,5) / 3000 = 0,0015
Vi får derved funktionsforskriften y = 0,0015x + 5,5

Eksempel: Isbod med lineært faldende grænseomkostninger

Her ser vi på en isbod, hvor grænseomkostningerne falder gradvist liniært med produktionen:

Mængde X stk. afsætning	Gromk
0 stk.	10,5 kr
1000 stk.	9 kr
2000 stk.	7,5 kr
3000 stk.	6 kr

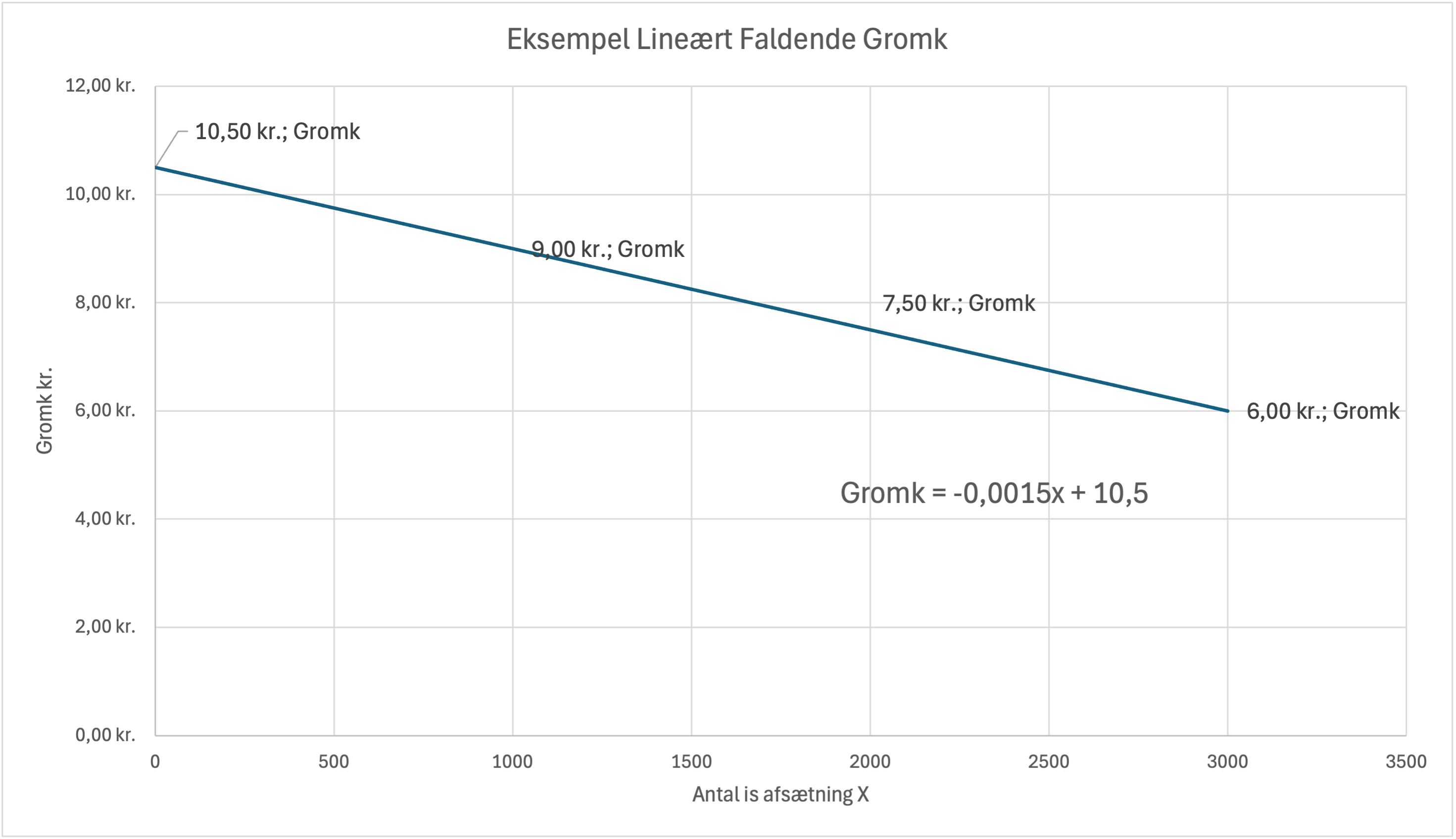
Vi kan bestemme funktionsforskriften for grænseomkostningerne ved at indsætte punkterne i f.eks. Excel og tilføje en trendlinje.
Vi kan også udregne funktionsforskriften når vi har to punkter.
Eksempelvis har vi punkterne (0,10,5) og (3000,6)
Vi indsætter punkterne i formlen for en lineær funktion y = ax + b
Vi får derved ligningen 10,5 = a*0 + b, hvor vi kan se, at b = 10,5
Vi får derved ligningen 6 = a*3000 + 10,5, hvor vi kan løse for a
a = (6-10,5) / 3000 = -0,0015
Vi får derved funktionsforskriften y = -0,0015x + 10,5

Vigtige overvejelser ved forskellige omkostningsforløb

Trappeformede grænseomkostninger opstår ofte ved overarbejde eller mængderabat
Lineært stigende grænseomkostninger kan skyldes ineffektivitet ved høj produktion
Lineært faldende grænseomkostninger kan skyldes læringseffekter eller stordriftsfordele
Det er vigtigt at kende grænseomkostningernes forløb for at kunne optimere produktionen

Beslutningsrelevans

Beslutningsrelevante omkostninger er de omkostninger, der er relevante for en specifik beslutning. Det er kun de omkostninger, der ændrer sig som følge af beslutningen, der skal indgå i beslutningsgrundlaget. Dette er en vigtig faktor i beslutningstagning, da det hjælper med at fokusere på de relevante omkostninger.

Virksomhed	Beslutning	Beslutningsrelevante omkostninger	Forklaring
LEGO	Lancere ny serie	Produktionsomkostninger, markedsføring	Kun de omkostninger der ændrer sig ved lanceringen
Tesla	Bygge ny fabrik	Byggeomkostninger, nye medarbejdere	Kun de omkostninger der opstår ved den nye fabrik
NVIDIA	Udvide produktion	Ekstra råvarer, overarbejde	Kun de variable omkostninger ved udvidelsen
Novo Nordisk	Udvide forskning	Nye forskere, udstyr	Kun de omkostninger der opstår ved udvidelsen
Carlsberg	Ændre emballage	Nye emballageomkostninger	Kun forskellen i emballageomkostninger
H&M	Åbne ny butik	Butiksleje, nye medarbejdere	Kun de omkostninger der opstår ved den nye butik

Eksempel: Isbod med beslutningsrelevante omkostninger

Lad os se på forskellige beslutninger i en isbod og deres beslutningsrelevante omkostninger:

Beslutning	Beslutningsrelevante omkostninger	Forklaring
Udvide åbningstid	Ekstra løn, strøm, is	Kun de omkostninger der ændrer sig ved udvidelsen
Købe ny ismaskine	Købspris, ekstra strøm	Kun de omkostninger der opstår ved den nye maskine
Ændre is-sorter	Forskel i råvareomkostninger	Kun forskellen i omkostninger mellem sorterne
Ansætte ekstra medarbejder	Løn, uniform, træning	Kun de omkostninger der opstår ved den nye medarbejder

Vigtige overvejelser ved beslutningsrelevante omkostninger

Kun de omkostninger der ændrer sig skal indgå i beslutningen
Faste omkostninger er ofte ikke beslutningsrelevante
Det er vigtigt at identificere alle relevante omkostninger
Beslutningsrelevante omkostninger kan være både faste og variable

Irrelevante omkostninger (Sunk Costs)

Vi har tidligere set på begrebet sunk costs i mikroøkonomi. Irrelevante omkostninger er omkostninger, der allerede er opstået og ikke kan påvirkes af fremtidige beslutninger. Disse omkostninger skal ikke indgå i beslutningsgrundlaget, da de ikke påvirker den fremtidige økonomi.

Virksomhed	Beslutning	Irrelevante omkostninger	Forklaring
LEGO	Lancere ny serie	Udgifter til tidligere forskning	Disse omkostninger er allerede opstået og kan ikke påvirkes
Tesla	Bygge ny fabrik	Udgifter til tidligere markedsundersøgelser	Disse omkostninger er sunk costs og skal ikke indgå i beslutningen
NVIDIA	Udvide produktion	Afskrivninger på eksisterende maskiner	Disse omkostninger er allerede opstået og kan ikke ændres
Novo Nordisk	Udvide forskning	Udgifter til tidligere kliniske studier	Disse omkostninger er sunk costs og skal ikke indgå i beslutningen
Carlsberg	Ændre emballage	Udgifter til tidligere emballagedesign	Disse omkostninger er allerede opstået og kan ikke påvirkes
H&M	Åbne ny butik	Udgifter til tidligere markedsanalyse	Disse omkostninger er sunk costs og skal ikke indgå i beslutningen

Eksempel: Isbod med irrelevante omkostninger

Lad os se på forskellige beslutninger i en isbod og deres irrelevante omkostninger:

Beslutning	Irrelevante omkostninger	Forklaring
Udvide åbningstid	Afskrivninger på eksisterende ismaskine	Disse omkostninger er allerede opstået og kan ikke ændres
Købe ny ismaskine	Udgifter til tidligere reparationer af gammel maskine	Disse omkostninger er sunk costs og skal ikke indgå i beslutningen
Ændre is-sorter	Udgifter til tidligere markedsundersøgelser	Disse omkostninger er allerede opstået og kan ikke påvirkes
Ansætte ekstra medarbejder	Udgifter til tidligere medarbejdertræning	Disse omkostninger er sunk costs og skal ikke indgå i beslutningen

Vigtige overvejelser ved irrelevante omkostninger

Irrelevante omkostninger er allerede opstået og kan ikke påvirkes
De skal ikke indgå i beslutningsgrundlaget
Det er vigtigt at kunne skelne mellem relevante og irrelevante omkostninger
Irrelevante omkostninger kan være svære at ignorere psykologisk

Offeromkostninger

Offeromkostninger har vi tidligere set på i mikroøkonomi, det er en beslutningsorienteret omkostningsdefinition, der fokuserer på det man ofrer ved at vælge én handling frem for en alternativ handling.
Offeromkostninger kaldes også opportunity costs eller alternativomkostninger.

Virksomhed	Beslutning	Offeromkostning	Forklaring
LEGO	Bygge ny fabrik	Mistet renteindtægt på investeringen	LEGO ofrer den renteindtægt de kunne have fået ved at placere pengene i banken
Tesla	Bygge ny Gigafactory	Mistet udvikling af selvkørende teknologi	Tesla ofrer den udvikling de kunne have opnået ved at investere i forskning i stedet
NVIDIA	Fokusere på AI-chips	Mistet salg af gaming-grafikkort	NVIDIA ofrer det salg de kunne have fået på deres eksisterende gaming-produkter
Novo Nordisk	Udvide insulinproduktion	Mistet udvikling af nye diabetesmediciner	Novo Nordisk ofrer den innovation de kunne have opnået ved at fokusere på forskning
Carlsberg	Lancere nyt øl	Mistet salg af eksisterende øl	Carlsberg ofrer det salg de kunne have fået på deres eksisterende øl
H&M	Åbne ny butik	Mistet lejeindtægt	H&M ofrer den lejeindtægt de kunne have fået ved at udleje lokalerne

Eksempel: Isbod med offeromkostninger

Lad os se på en isbod, hvor ejeren overvejer at udvide åbningstiden:

Beslutning	Offeromkostning	Værdi
Udvide åbningstid med 2 timer	Mistet fritid	500 kr. (værdi af fritid)
Ansætte ekstra medarbejder	Mistet overskud på egen arbejdskraft	200 kr. pr. time
Købe ny ismaskine	Mistet renteindtægt på investeringen	50.000 kr. × 5% = 2.500 kr. pr. år

Vigtige overvejelser ved offeromkostninger

Offeromkostninger er relateret til en specifik beslutning
De inkluderer både direkte omkostninger og mistede muligheder
Offeromkostninger er ikke altid lette at kvantificere
De er vigtige at overveje ved strategiske beslutninger

Reversibilitet

Reversibilitet refererer til hvor nemt og kostbart det er at ændre en beslutning. En beslutning er reversibel, hvis den kan ændres uden store omkostninger eller tab. Dette er en vigtig faktor i beslutningstagning, da det påvirker risikoen ved forskellige valg.

Virksomhed	Beslutning	Reversibilitet	Forklaring
LEGO	Ændre produktdesign	Høj	Let at ændre design før produktion starter, lav omkostning ved ændring
Tesla	Bygge ny fabrik	Lav	Meget kostbart at ændre eller nedlægge en færdigbygget fabrik
NVIDIA	Ændre chip-design	Medium	Kostbart at ændre under produktion, men muligt før masseproduktion
Novo Nordisk	Udvide produktion	Lav	Meget kostbart at nedlægge eller ændre medicinalproduktion
Carlsberg	Ændre øl-recept	Medium	Kan ændres, men kræver ny godkendelse og markedsføring
H&M	Ændre kollektion	Høj	Let at ændre design og produktion, lav omkostning ved ændring

Eksempel: Isbod med reversibilitet

Lad os se på forskellige beslutninger i en isbod og deres reversibilitet:

Beslutning	Reversibilitet	Omkostning ved ændring
Introducere lakridschili-is	Høj	Kun omkostningerne ved at købe nye varer
Ændre åbningstider	Høj	Minimale omkostninger, kun personaleprogram
Købe ny ismaskine	Lav	Stor tab ved salg af brugt maskine
Ændre priser	Høj	Kun omkostninger ved ny prisskilt

Vigtige overvejelser ved reversibilitet

Høj reversibilitet giver mere fleksibilitet og mindre risiko
Lav reversibilitet kræver mere grundig analyse før beslutning
Reversibilitet påvirker virksomhedens evne til at tilpasse sig ændringer
Det er vigtigt at overveje reversibilitet ved store investeringer

Specielle omkostningsfunktioner

I den virkelige verden vil vi sjældent se en omkostningsfunktion, der er konstante eller lineære funktioner specielt hvis man har med mere komplekse produktionsprocesser at gøre. Når vi i de følgende kapitler regner på for at bestemme den optimale pris og afsætning benytter vi disse noget forenklede omkostningsfunktioner.
Omkostningsfunktioner vil dog i virkeligheden kan have forskellige forløb afhængigt af, hvordan omkostningerne udvikler sig i forhold til produktionsmængden.

Vi skelner mellem tre hovedtyper:

Degressive funktioner: Omkostningerne stiger mindre end proportionalt med mængden (faldende grænseomkostninger)
Konstante funktioner: Omkostningerne stiger proportionalt med mængden (konstante grænseomkostninger)
Progressive funktioner: Omkostningerne stiger mere end proportionalt med mængden (stigende grænseomkostninger)

Eksempel: Vinmarksejerens Omkostninger

Lad os følge en vinmarksejer, der skal producere vin. Processen involverer flere trin:

Plukke druer
Stampe druer (uden sko på!)
Fermentere mosten
Flaskesætte vinen

Omkostningerne udvikler sig forskelligt afhængigt af antal medarbejdere:

Antal medarbejdere	Omkostninger pr. flaske	Forklaring
1	125 kr.	Bonden plukker først druerne, tager sko og sokker af, tramper rundt i druerne, vasker fødder, tager sko på igen, går ud og plukker flere druer, tager sko af igen, tramper... og sådan fortsætter det hele dagen. Det tager lang tid!
2	100 kr.	Nu kan den ene plukke druer mens den anden tramper. Det går meget bedre, men de skal stadig vente på hinanden, når de skifter opgaver.
3	80 kr.	Optimal arbejdsdeling! Den ene plukker, den anden tramper, og den tredje flaskesætter. Ingen ventetid, perfekt flow!
4	85 kr.	Nu begynder det at blive trangt i vinkælderen. De står og snakker om fodbold og går i vejen for hinanden. Den ene spilder most på gulvet fordi den anden skubber til ham.
5	155 kr.	Kaos! Alle snakker på én gang, ingen kan høre hinanden, og der er druer over det hele. Den ene spilder en hel tønde most fordi han vender sig for hurtigt og rammer den anden i ryggen. Det er blevet en dyr fornøjelse!

Dette eksempel viser:

Degressive omkostninger: Fra 1 til 3 medarbejdere falder omkostningerne pr. flaske - det går fra at være en enkelt træt bonde til et velorganiseret team
Progressive omkostninger: Fra 3 til 5 medarbejdere stiger omkostningerne pr. flaske - det bliver for mange kokke i køkkenet!
Optimalt antal: 3 medarbejdere giver de laveste omkostninger pr. flaske - det er det perfekte antal for en lille vinproduktion

Virksomhed	Omkostningstype	Eksempel	Forklaring
Tesla	Progressiv	Produktion af Model Y	Ved høj produktion stiger omkostningerne mere end proportionalt pga. overarbejde, ekstra skift og øget kvalitetskontrol
Novo Nordisk	Progressiv	Insulinproduktion	Når produktionen nærmer sig kapacitetsgrænsen, stiger omkostningerne til kvalitetssikring og validering markant
LEGO	Progressiv	Specialklodser	Ved produktion af særlige farver/former stiger omkostningerne pga. hyppigere maskinomstilling og mindre batchstørrelser
H&M	Konstant	T-shirt produktion	Fast pris pr. t-shirt fra leverandører uanset ordrestørrelse
Carlsberg	Konstant	Standardøl	Faste råvarepriser og standardiseret produktionsproces giver konstante omkostninger pr. flaske
McDonald's	Konstant	Big Mac	Standardiserede ingredienser og processer giver samme omkostning pr. burger
NVIDIA	Degressiv	GPU-produktion	Faldende enhedsomkostninger pga. læringskurve og optimering af produktionsprocesser
Mærsk	Degressiv	Containertransport	Jo flere containere der transporteres, jo lavere bliver omkostningen pr. container
Netflix	Degressiv	Streaming	Marginale omkostninger pr. bruger falder med antal brugere pga. bedre udnyttelse af serverkapacitet

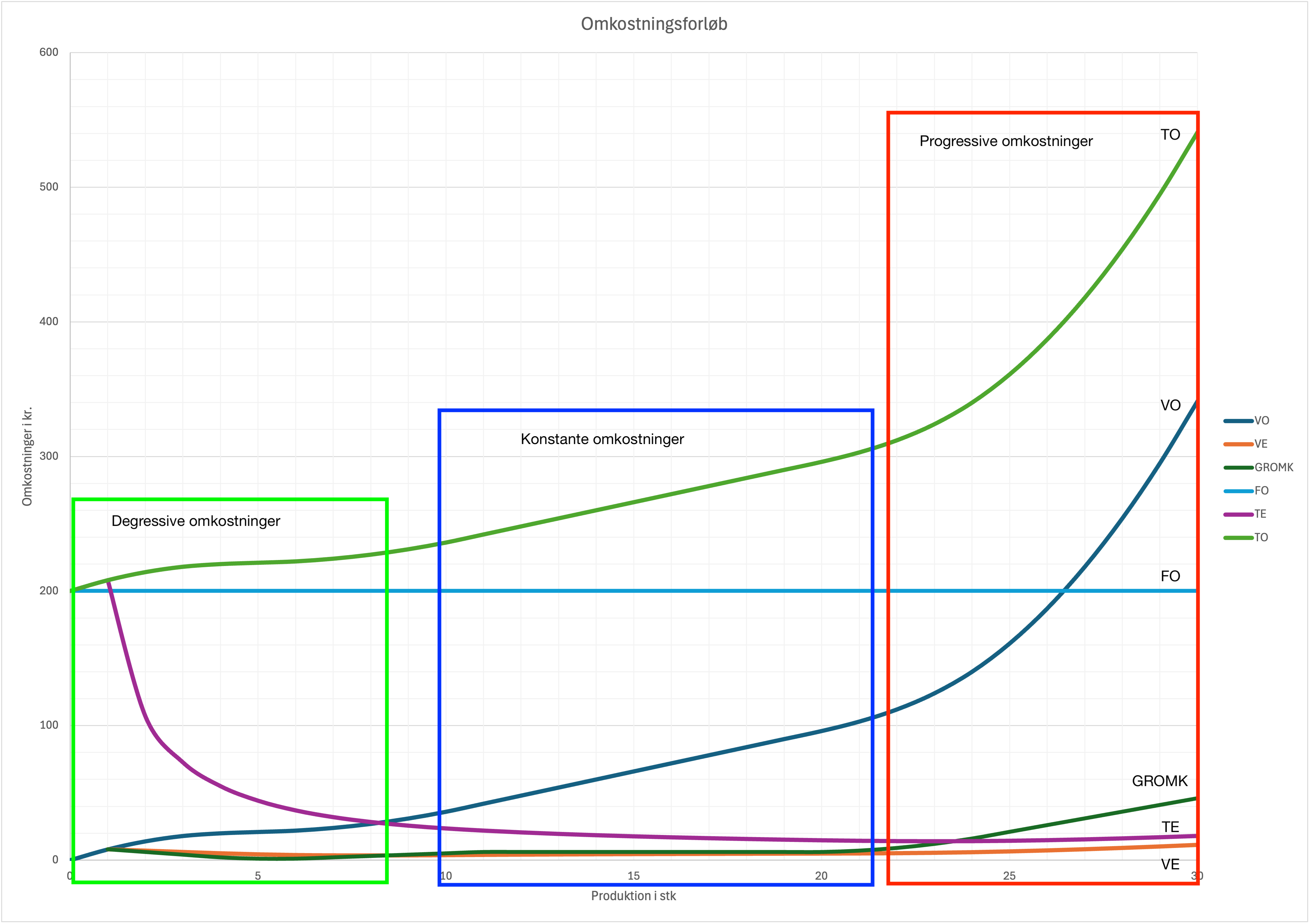
Eksempel

Mængde (X)	Variable Omk. (VO)	Variable Enheds. (VE)	Grænseomk. (GROMK)	Faste Omk. (FO)	Total Enheds. (TE)	Totale Omk. (TO)
0	0	-	-	200	-	200
5	21	4,2	1	200	44,2	221
10	36	3,6	5	200	23,6	236
15	66	4,4	6	200	17,73	266
20	96	4,8	6	200	14,8	296
25	161	6,44	21	200	14,44	361
30	341	11,37	46	200	18,03	541

Analyse af omkostningsfunktionerne:

1. Degressive omkostninger (0-10):

Variable enhedsomkostninger falder fra 4,2 kr. til 3,6 kr.
Indikerer stordriftsfordele i opstartsfasen
Totale enhedsomkostninger falder markant pga. bedre udnyttelse af faste omkostninger

2. Konstante omkostninger (10-20):

Grænseomkostningerne er relativt stabile omkring 6 kr.
Variable enhedsomkostninger ligger mellem 3,6-4,8 kr.
Repræsenterer optimal produktionskapacitet

3. Progressive omkostninger (20-30):

Grænseomkostningerne stiger kraftigt fra 6 kr. til 46 kr.
Variable enhedsomkostninger stiger fra 4,8 kr. til 11,37 kr.
Indikerer kapacitetsbegrænsninger i produktionen

Degressive omkostninger (0-10 enheder)

I intervallet 0-10 enheder ser vi et typisk degressivt omkostningsforløb, hvor omkostningerne stiger mindre end proportionalt med mængden. Dette betyder:

Variable enhedsomkostninger falder fra 4,2 kr. til 3,6 kr.
Grænseomkostningerne er lavere end de variable enhedsomkostninger
Hver ny enhed er billigere at producere end den forrige

Dette mønster er typisk i opstartsfasen, hvor virksomheden gradvist bliver mere effektiv til at udnytte sine ressourcer. Årsager til degressive omkostninger kan være:

Bedre udnyttelse af produktionsudstyr
Medarbejdere bliver mere rutinerede
Optimering af arbejdsprocesser
Mængderabatter på råvarer

Konstante omkostninger (10-20 enheder)

I intervallet 10-20 enheder observerer vi et konstant omkostningsforløb, hvor omkostningerne stiger proportionalt med mængden. Dette betyder:

Variable enhedsomkostninger er stabile mellem 3,6-4,8 kr.
Grænseomkostningerne er konstante omkring 6 kr.
Hver ny enhed koster det samme at producere som den forrige

Dette interval repræsenterer den optimale produktionskapacitet, hvor:

Produktionen kører mest effektivt
Der er balance mellem kapacitet og efterspørgsel
Ressourceudnyttelsen er optimal
Produktionsprocessen er stabil og forudsigelig

Progressive omkostninger (20-30 enheder)

I intervallet 20-30 enheder ser vi et progressivt omkostningsforløb, hvor omkostningerne stiger mere end proportionalt med mængden. Dette betyder:

Variable enhedsomkostninger stiger fra 4,8 kr. til 11,37 kr.
Grænseomkostningerne stiger drastisk fra 6 kr. til 46 kr.
Hver ny enhed er dyrere at producere end den forrige

Dette mønster opstår typisk når virksomheden nærmer sig sin kapacitetsgrænse. Årsager til progressive omkostninger kan være:

Overarbejdsbetaling til medarbejdere
Slid på maskiner der kræver mere vedligeholdelse
Flaskehalse i produktionen
Kvalitetsproblemer pga. presset produktion

Stordriftsfordele (Economies of Scale)

Som vi kan se i tallene ovenfor, opnås de bedste stordriftsfordele i produktionsintervallet 10-20 enheder, hvor omkostningerne er mest effektive. Dette kan skyldes flere faktorer:

Produktionsinterval	Omkostningstype	Forklaring
0-10 enheder	Degressiv	Opstartsfordele og bedre kapacitetsudnyttelse
10-20 enheder	Konstant	Optimal produktion med stabile omkostninger
20-30 enheder	Progressiv	Kapacitetsgrænsen nås, hvilket øger omkostningerne

Vigtige observationer fra tallene:

De totale enhedsomkostninger (TE) falder frem til 25 enheder, hvorefter de stiger igen
Grænseomkostningerne (GROMK) er lavest i starten og stiger drastisk efter 20 enheder
Variable enhedsomkostninger (VE) finder deres minimum omkring 10 enheder
Den optimale produktion ligger omkring 20 enheder, hvor man balancerer stordriftsfordele med stigende omkostninger

Alle omkostninger bliver variable på langt sigt

En vigtig økonomisk lov er, at alle omkostninger bliver variable på langt sigt. Dette betyder, at selv de mest faste omkostninger på et tidspunkt kan ændres eller elimineres. Her er nogle eksempler:

Kort sigt	Langt sigt	Forklaring
Fast husleje	Variabel	Virksomheden kan flytte til billigere lokaler eller nedlægge afdelingen
Fast løn til medarbejdere	Variabel	Virksomheden kan fyre medarbejdere eller ændre deres arbejdstid
Afskrivninger på maskiner	Variabel	Virksomheden kan sælge maskinerne eller skifte til billigere alternativer
Forsikringer	Variabel	Virksomheden kan ændre forsikringsdækningen eller skifte forsikringsselskab

Vigtige overvejelser ved langtidsplanlægning:

På langt sigt kan virksomheden tilpasse alle sine ressourcer
Dette giver mere fleksibilitet i beslutningstagningen
Virksomheden kan optimere sin kapacitet og omkostningsstruktur
Det er vigtigt at have en langtidsplan for omkostningsstyring

Quiz

Quiz om erhvervsøkonomi