Pris, Afsætning og Omsætning

Pris, Afsætning og Omsætning

Prisen er en af de vigtigste faktorer for en virksomheds succes. I dette kapitel vil vi se på, hvordan prisen påvirker afsætningen og omsætningen.

Vi vil i dette kapitel fokusere på:

  • Prisafsætningsfunktionen og dens betydning
  • Omsætningen

Prisens betydning for forbrugerens efterspørgsel

Prisen har en direkte indflydelse på forbrugerens efterspørgsel. Generelt gælder at:

  • Jo højere pris, jo lavere efterspørgsel
  • Jo lavere pris, jo højere efterspørgsel
  • Dette er kendt som loven om efterspørgsel

Faktorer der påvirker efterspørgslen:

  • Prisen på varen
  • Forbrugerens indkomst
  • Prisen på alternative varer
  • Forbrugerens præferencer
  • Antal potentielle købere


Prisafsætningsfunktionen

I økonomi bruger vi ofte en forenklet lineær prisafsætningsfunktion til at beskrive sammenhængen mellem pris og afsætning. Denne funktion er givet ved:

P = aX + b

hvor:

  • P er prisen
  • X er afsætningsmængden, nogle bøger kalder afsætningen for Q eller M.
  • a er hældningskoefficienten (negativ værdi)
  • b er skæringspunktet med y-aksen (maksimal pris)
  • Bemærk vi har X afsætningen på X-aksen og P prisen er på Y-aksen.
    Intuitivt, ville vi sige at prisen er en parameter virksomheden styrer og derved påvirker afsætningen, men historisk set har det været afsætningen på X-aksen og prisen på Y-aksen.

Eksempel på prisafsætningsfunktion:

For en isbod kunne prisafsætningsfunktionen pr. time være:

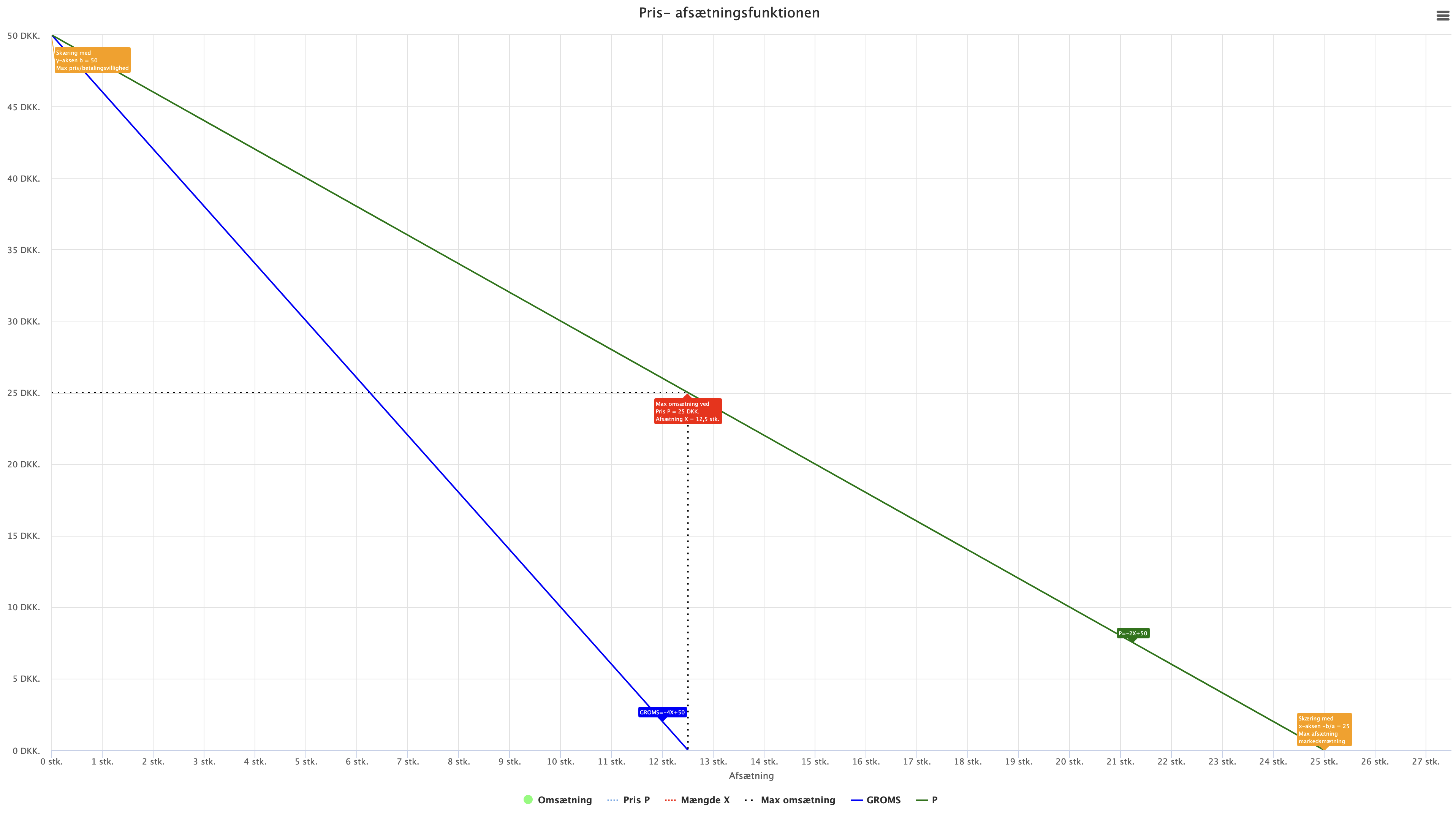
P = -2X + 50

Dette betyder at:

  • Den maksimale pris er 50 kr. (når afsætningen X = 0) Det betyder at når prisen er 50 kr. er der ikke nogen der vil købe is, punktet (0,50) er markeret med en orange tekstboks i figuren nedenfor.
  • For hver is mere der sælges, falder prisen med 2 kr.
  • Ved en pris på 0 kr. vil der blive solgt 25 is, dette er den maksimale afsætning, dette kunne være begrænset af efterspørgslen, eller at virksomheden ikke kan producere flere is indenfor den time vi ser på.
  • Bemærk at vi har en negativ hældning, hvilket betyder at jo højere pris jo lavere afsætning.
  • I figuren nedenfor kan vi se den grønne linje, som er prisafsætningsfunktionen.
    Bemærk at den er aftagende starter i (0,50) hvor ingen vil købe isen og skærer X-aksen i (25,0) ved den maksimale afsætning.
  • Når prisafsætningsfunktionen P er lineær som her, gælder altid at skæringen med X-aksen dvs. den maksimale afsætning kan beregnes som -b/a = -50/(-2) = 25 stk. Dette er markeret med en orange tekstboks i figuren nedenfor.
  • Når prisafsætningsfunktionen P er lineær som her, gælder altid at prisen der maksimerer omsætningen er halvdelen af den maksimale pris b, dvs. b/2 = 50/2 = 25 kr. Dette er markeret med en rød tekstboks i figuren nedenfor.
Prisafsætningsfunktion

Du kan selv hente appen nedenfor og prøve at ændre på parametrene a og b i prisafsætningsfunktionen:
App til prisafsætningsfunktion
Prisafsætningsfunktion

Omsætning

Vi kan ud fra prisafsætningsfunktionen beregne omsætningen. Vi kan jo allerede afgøre at ved priserne 0 kr. og 50 kr. er omsætningen 0. Omsætningen er jo pris gange afsætning, dvs. 50*0 = 0 kr. og 0*25 = 0 kr. Vi kan bestemme alle mulige omsætninger ved at indsætte forskellige priser i prisafsætningsfunktionen, og gange med den tilsvarende pris.
Men det er nemmere at gange prisafsætningsfunktionen med X, dvs. P*X.
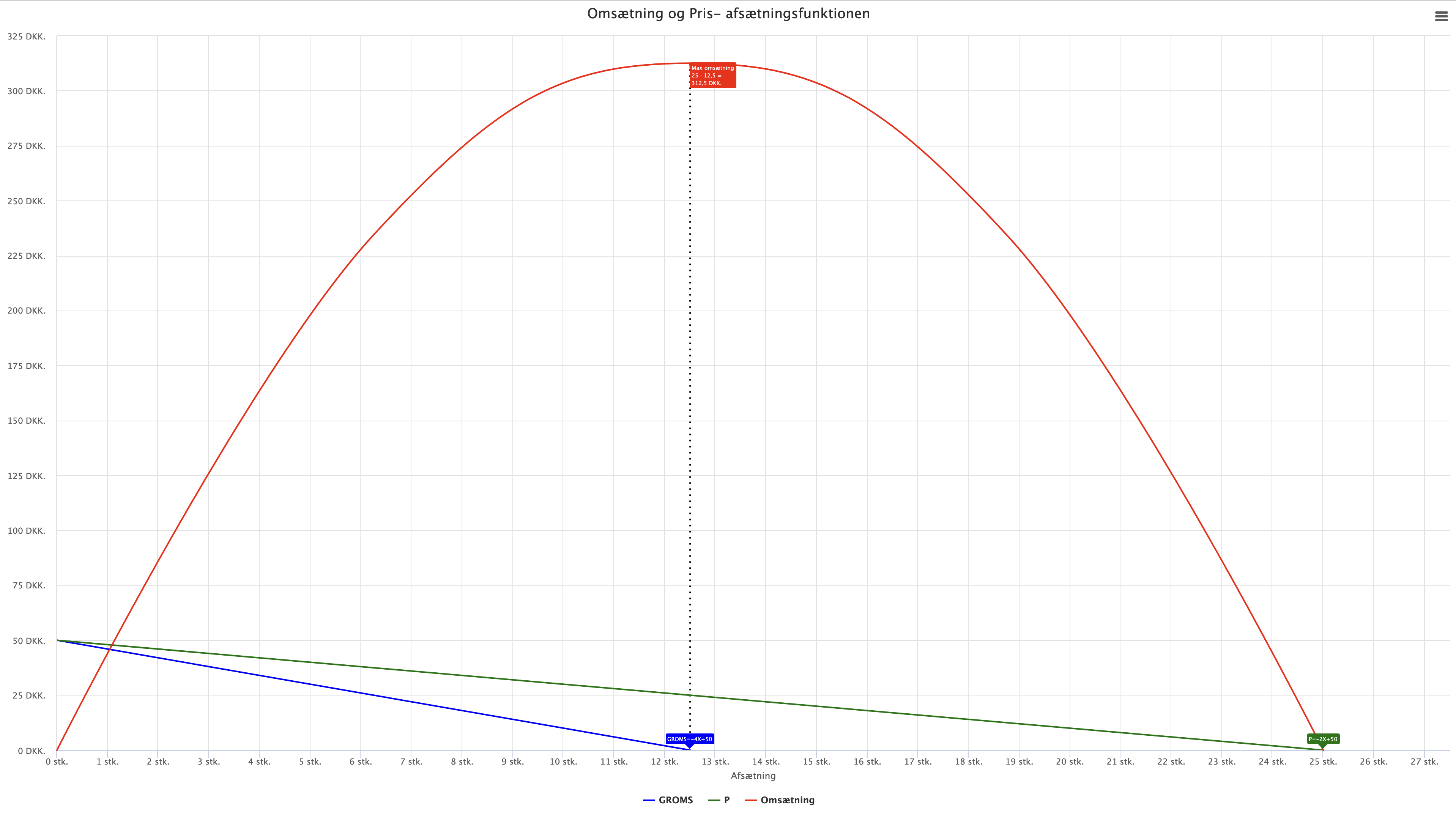
Omsætning = P*X = (-2X + 50)*X = -2X2 + 50X
Omsætningen (den røde kurve) ses også i appen sammen med prisafsætningsfunktionen (den grønne kurve):
Omsætningen er altid et 2. gradspolynomium, når prisafsætningsfunktionen er lineær.
Omsætningen er maksimal i toppunktet, som ses i figuren nedenfor, markeret med en rød tekstboks. Den maksimale omsætning opnås når afsætningen er 12,5 stk. og prisen er 25 kr., dvs. omsætningen er 12,5*25 = 312,5 kr.
Husk på, at den pris der maksimerer omsætningen er i udgangspunktet for lav - virksomheder ønsker at maksimere dækningsbidraget IKKE omsætningen. På kortere sigt kan virksomheden af konkurrencehensyn ønske at sætte prisen lavt for at presse konkurrenten ud af markedet eller øge markedsandelen.

Omsætning

Grænseomsætning

Ligesom vi tidligere så på grænseomkostningen, kan vi også se på grænseomsætningen. Grænseomsætningen er den ændring i omsætningen, når afsætningen ændres med 1 enhed.
Grænseomsætningen er altså den afledte af omsætningen. Grænseomsætningen er den lineære blå kurve i figuren ovenfor.

Grænseomsætningen er den afledte af omsætningen, dvs.

Groms = Omsætning' = (-2X2 + 50X)' = 2·-2X2-1 + 1·50X1-1 = -4X + 50

Hver gang vi har en lineær prisafsætningsfunktion, har vi også en lineær grænseomsætning.
Hvis den lineære prisafsætningsfunktion P = aX + b, har vi Groms = 2aX + b.
Dvs. Groms er en lineær funktion med dobbelt hældning af P.
Bemærk, der er samme forhold mellem P og Groms, som der er mellem VE og Gromk, som vi så på tidligere.
For isboden havde vi P = -2X + 50, så Groms = 2·-2X + 50 = -4X + 50.
Vi kan altså hurtigt finde grænseomsætningen, hvis vi kender prisafsætningsfunktionen og denne er lineær.

Den blå kurve i appen er grænseomsætningen, ses også i appen sammen med prisafsætningsfunktionen (den grønne kurve).
Bemærk, at grænseomsætningen har samme skæringspunkt med Y-aksen som prisafsætningsfunktionen, da både omsætningen og grænseomsætningen skærer Y-aksen i (0,b) = (0,50).
Da grænseomsætningen har den dobbelte hældning af prisafsætningsfunktionen, vil grænseomsætningen skære X-aksen dobbelt så hurtigt som prisafsætningsfunktionen.
Vi så tidligere, at prisafsætningsfunktionen for isboden skærer X-aksen i (-b/a;0) = (25;0),
dvs. grænseomsætningen skærer X-aksen i (-b/2a;0) = (12,5;0).
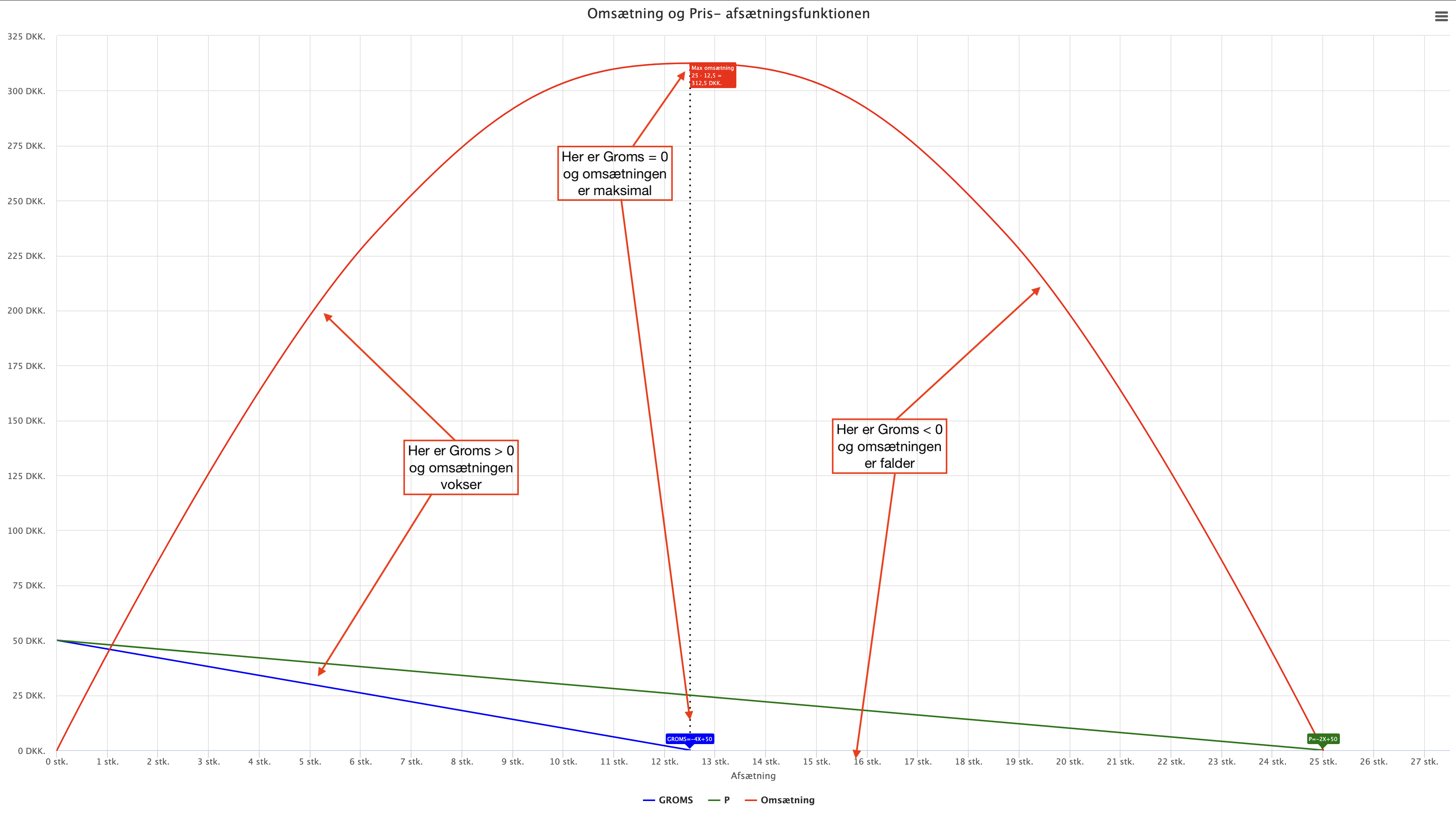
Grænseomsætningen har altså positive funktionsværdier for alle X mellem 0 og 12,5, er 0 når X = 12,5 og er derefter negativ.
Dette passer præcis med, at omsætningen stiger for X mellem 0 og 12,5, er maksimal i X = 12,5 og falder for X større end 12,5.
Grænseomsætningen angiver jo tangenthældningen til omsætningen, og den er stigende for X mellem 0 og 12,5, maksimal i X = 12,5 og falder for X større end 12,5.


Grænseomsætning

Vi kan undersøge om sammenhængen mellem omsætningen og grænseomsætningen passer ved at indsætte forskellige værdier i Groms = -4X + 50

  • For X = 0, er Groms = -4·0 + 50 = 50
    Når afsætningen X vokser fra 0 til 1 stk., så stiger omsætningen med ca. 50 kr.
  • For X = 1, er Groms = -4·1 + 50 = 46
    Når afsætningen X vokser fra 1 til 2 stk., så stiger omsætningen med ca. 46 kr.
  • For X = 12,5, er Groms = -4·12,5 + 50 = 0
    Når omsætningen er maksimal, er grænseomsætningen 0.
  • For X = 20, er Groms = -4·20 + 50 = -30
    Når afsætningen X vokser fra 20 til 21 stk., så falder omsætningen med ca. 30 kr.

Bemærk, vi skriver at omsætningen stiger eller falder med cirka dette beløb. Vi ændrer afsætningen med 1 hel enhed, men tangenthældningen gælder i virkeligheden kun for meget små ændringer i afsætningen ΔX.

Prisændringer og Deres Effekt - Eksempler fra Virkelige Virksomheder

Virksomhed Produkt Prisændring Ændring i Afsætning Ændring i Omsætning Grænseomsætning Konsekvens
Netflix Premium Abonnement +20 kr. (159 → 179 kr.) -5% +13% Positiv Øget overskud på trods af færre abonnenter
Spotify Student Abonnement -20 kr. (69 → 49 kr.) +40% +15% Positiv Øget markedsandel og omsætning gennem lavere pris
Apple iPhone 15 Pro +1.000 kr. (11.999 → 12.999 kr.) -8% +3% Positiv Højere dækningsbidrag pr. enhed
McDonald's Big Mac Menu +5 kr. (85 → 90 kr.) -2% +4% Positiv Øget omsætning på trods af færre kunder
Zalando Standard Levering +29 kr. (0 → 29 kr.) -15% -8% Negativ Fald i omsætning på grund af høj priselasticitet

Vigtige observationer:

  • Netflix og Apple viser eksempler på inelastisk efterspørgsel, hvor prisstigninger giver øget omsætning
  • Spotify demonstrerer priselasticitet, hvor prisreduktioner kan øge omsætningen gennem større afsætning
  • McDonald's viser en balance mellem pris og afsætning med moderat priselasticitet
  • Zalando's eksempel viser risikoen ved prisstigninger på services med høj priselasticitet

Quiz

Quiz om erhvervsøkonomi